What is amortization? Definition and examples

Amortization is a term people commonly use in finance and accounting. However, the term has several different meanings depending on the context of its use.

Amortization may refer to the liquidation of an interest-bearing debt through a series of periodic payments over a certain period. In most cases, the payments over the period are of equal amounts. Paying in equal amounts is actually quite common when taking out a loan or a mortgage.

Harvard Business School has the following definition of ‘amortization’:

“Amortization is a method of spreading an intangible asset’s cost over the course of its useful life. Intangible assets are non-physical assets that are essential to a company, such as a trademark, patent, copyright, or franchise agreement.”

Amortization vs. depreciation

The two words are very similar and are used in accounting. Here is the difference:

  • Amortization

We use amortization for intangible assets, such as software, trademarks, patents, copyrights, customer lists, and franchise agreements. They do not deteriorate physically, however, they may lose value as they near the end of their legal or useful life.

  • Depreciation

We use depreciation for tangible assets, i.e., ones we can touch, such as equipment, vehicles, and buildings. These assets deteriorate over time.

Amortization of loans

An amortization schedule determines the distribution of payments of a loan into cash flow installments. As opposed to other models, the amortization model comprises both the interest and the principal.

Amortization is one of the simplest repayment models there are. It is very simple because the borrower pays the repayments in equal amounts during the loan’s lifetime.

Typically, more money is applied to interest at the start of the schedule. Towards the end of the schedule, on the other hand, more money is applied to the principal.

We amortize a loan when we use a part of each payment to pay interest. Subsequently, we use the remaining part to reduce the outstanding principal.

Over time, after the series of payments, the borrower gradually reduces the outstanding principal. Additionally, interest on the unpaid balance falls.

Once a debt is amortized by equal payments at equal intervals, the debt becomes an annuity’s discounted value.

We use amortization tables to represent the composition of periodic payments between interest charges and principal repayments.

Negative amortization can occur if the payments fail to match the interest. In this case, the lender then adds outstanding interest to the total loan balance. As a consequence of adding interest, the total loan amount becomes larger than what it was originally.

The Amortization Schedule Formula

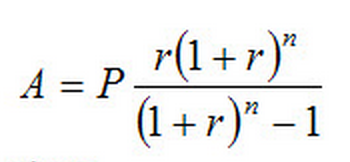
Amortization Schedule Formula
A = payment amount per period. P = initial principal (loan amount). r = interest rate per period. n = total number of payments or periods.

Calculating the amortization of a loan

You can calculate a loan’s payoff if you know:

  • The starting amount of the loan.
  • And also how many payments you will need to make.

An amortization table provides you with the principal and interest of each payment.

Assume that you have a ten-year loan of $10,000 that you pay back monthly. Also, assume that the annual percentage interest rate on this loan is 5%.

  • Step 1: How many repayments will you make?

In the example above, the loan is paid on a monthly basis over ten years. Therefore there is a total of (12 x 10) 120 loan payments.

  • Step 2: Calculate the period interest rate

To calculate the period interest rate you divide the annual percentage rate by the number of payments in a year.

In the example, payments are made on a monthly basis. Therefore, there are 12 payments each year. The annual interest rate is 5%. Therefore, the period interest rate would be (0.05/12) = 0.0041666, or 0.41667%.

  • Step 3: Use the Amortization Schedule Formula

You can use the amortization schedule formula to calculate the payment for each period.

In our example, the loan amount is $10,000. Our period interest rate is 0.00417. Our total number of payments is 120.

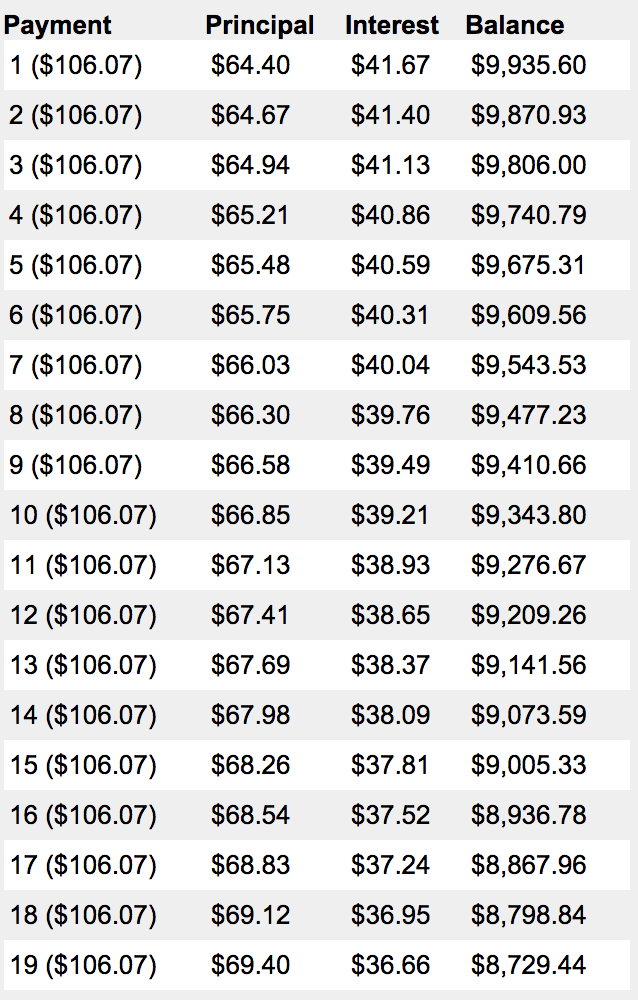
Amount per period = (10,000)*[(0.004166)((1+0.004166)^120)]/[(((1+0.004166)^120) -1)]

= $106.07

  • Step 4: Draw a table

Draw three columns. Give the first column the title of ‘Current Value’. Call the second column ‘Interest’, and the third column ‘Principal’.

In this example, you would write $10,000 at the top of the Current Value column.

  • Step 5: Calculate the Interest and Principal values and add them to your table

Multiply the current loan value by the period interest rate to get the interest. Then subtract the interest from the payment value to get the principal.

The “Interest” in the example would be: $10,000 * 0.00417 = $41.7

The Principal would be: $106.08 – $41.7 = 64.40

  • Step 6: Subtract the principal from the current value and write the new current value in the second row of the ‘Current Value’ column

$10,000 – 64.40 = $9935.60

  • Step 7: Repeat steps 5 and 6

In our example, the table would look like this. N.B. the table is not complete and only shows up to the 19th payment:

amortization

Amortization of intangible assets

Amortization also refers to the acquisition cost of intangible assets minus their residual value. In this sense, the term reflects the asset’s consumption and subsequent decline in value over time.

Amortization does not relate to some intangible assets, such as goodwill. Some intangible assets do not have a set period of ‘life’.

We record the amortization of intangible assets in the financial statements of a company as an expense.

The process of amortization not only affects a company’s financial statements but also has important tax implications, as the non-cash expense can reduce taxable income.

Compound nouns

In the world of accounting and finance, there are many compound nouns containing the word “amortization.” A compound noun is a term consisting of at least two words. Let’s take a look at some of them, their meanings, and how we can use them in a sentence:

  • Amortization Schedule

A table detailing each periodic payment on an amortizing loan, including amounts for principal and interest.
Example: “The mortgage advisor provided me with an amortization schedule to understand my payment breakdown over the years.”

  • Amortization Period

The total time period over which the principal amount of a debt is to be paid off through amortization.
Example: “The amortization period for their business loan was extended to 15 years to reduce monthly payments.”

  • Amortization Expense

The expense recognized in accounting for the gradual decrease in the carrying amount of an intangible asset.
Example: “The company’s income statement showed a significant amortization expense due to its recent acquisition of patents.”

  • Amortization Table

A tabular representation of the gradual decrease in the book value of an asset, similar to an amortization schedule.
Example: “I referred to the amortization table to calculate the remaining balance of my loan.”

  • Amortization Method

The formula or technique applied to calculate the amortization of an asset over its useful life.
Example: “They decided to use the straight-line amortization method for their new intellectual property investments.”

  • Amortization Calculator

A digital tool or software used to compute the amortization of a loan or asset.
Example: “To figure out my monthly car payments, I used an online amortization calculator.”

Video – What is Amortization?

This educational video, from our sister channel on YouTube – Marketing Business Network, explains what ‘Amortization’ is using simple and easy-to-understand language and examples.