What is a Zero-Sum Game? Definition and meaning

A Zero-Sum Game, which may have just two or up to millions of participants, is one in which one player’s gain is equivalent to another’s loss – therefore the net change in benefit or wealth is zero. When somebody wins in the game, another person loses the same amount, so that the winnings minus the losses equal zero.

Zero-sum games can be found in game theory and economic theory. They are, however, less common than non-zero-sum games. The adjective ‘zero-sum‘ originated in game theory in the 1940s.

In card games where people gamble, such as poker, the amount won by the winning player equals the combined losses of the losing players. Therefore, poker is a zero-sum game. If there is one winner and one loser – as in most games or contests such as tennis, chess, arm wrestling, or dominoes – it is a zero-sum game.

Zero-Sum Game
If one child gains an ice-cream and the other child loses one, the combined total is zero. The crying child above may have lost his ice-cream because the other kid stole it from him. (Image created by Market Business News)

Zero-sum games exist in financial markets – examples include options and futures (excluding transaction costs). For each party who gains on a contract, there is a counter-party who loses that same amount.

Zero- vs. non-zero sum games

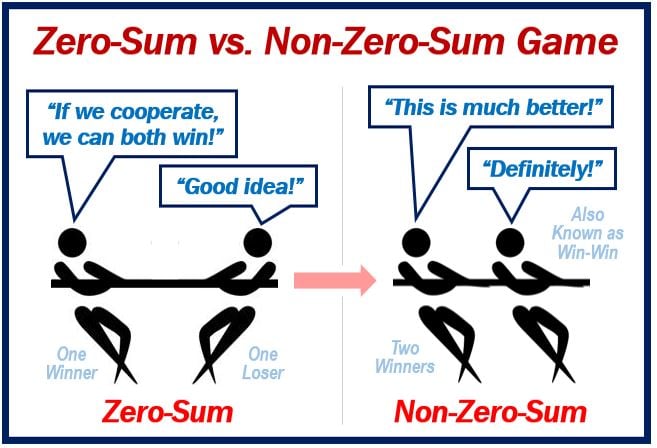
Zero-sum vs non-zero-sum game - image 4908308408
Image created by Market Business News.

A non-zero sum game is the opposite of a zero-sum game. When the interacting parties’ aggregate gains and losses are either less than or more than zero – but never exactly zero – it is a non-zero-sum game.

In economics, there are many situations that are non-zero-sum, since valuable goods and services can be created or destroyed – any of these games will create a net gain or loss of utility to several stakeholders.

When wealth is created, or additional benefits emerge, the total of one party’s gain is not exactly the total of another party’s loss.

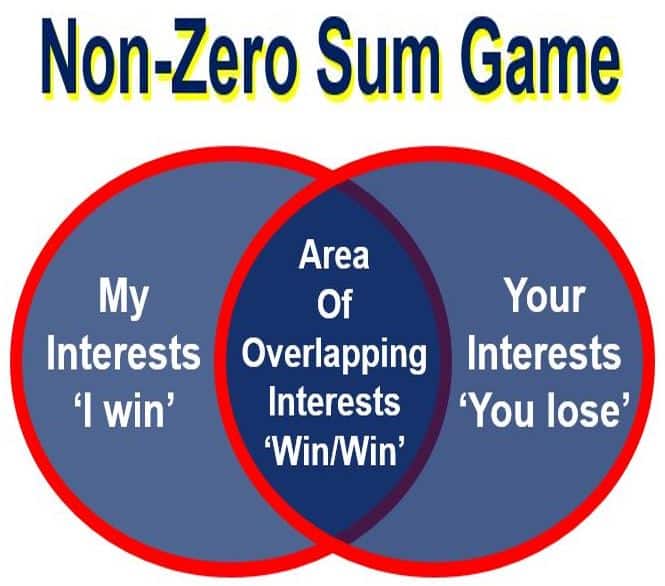
Non zero sum game
USALacrosse.org advises youth lacrosse coaches to make the sport a non-zero-sum game where the coaches of both teams acknowledge their divergent interests in the outcome of a match, which could include: fair play, respect for your opponent, playing to the best of your ability, honoring the game, and sportsmanship. (Image: adapted from uslacrosse.org)

All trade, in fact, by definition is a non-zero-sum-game, because when the buyer and seller agree to an exchange, each party must consider the goods or money it is receiving to be more valuable than the goods or money it is delivering.

Whenever an economic exchange occurs – with both parties acting freely – it must benefit them both to the point that each party can overcome the transaction costs. If not, they would never have entered the transaction.

Non-zero-sum games are non-strictly competitive, because they have both cooperative elements – it is not a question of it ending with one winner and loser. The players engaged in a non-zero-sum game have some complementary interests.

While zero-sum games are strictly competitive – there is one winner and one loser – it is possible for the players in a non-zero-sum game to both win, or both lose.

In a zero-sum game if there is no outright winner there might be a tie. In an arm-wrestling competition, both players or a referee may decide to call it a draw if enough time passes without one being able to beat the other.

Zero-sum games often not black and white

Many real life situations may look like winner-loser possibilities, but when you look at them more deeply you will find that it is not always the case. The pay-offs and losses in real life are not that easy to quantify.

Imagine you own a small business and have $2,000 to spare. You are trying to decide whether to reinvest it in your company or donate it to charity.

If you decide to reinvest it, the charity gets nothing. However, there is a chance that in the long-term the charity might gain. That $2,000 reinvestment could yield remarkable dividends, which allow you to donate much more than $2,000 at a later date.

If you decide to give the $2,000 to the charity, it may seem that the loser is your company. However, there may be some useful benefits in donating money that could help your business thrive. Your company’s reputation in the local community could improve, which may result in greater sales.

The Cambridge Dictionary has the following definition of zero-sum game:

“A situation in which an advantage that is won by one of two sides is lost by the other.”

In zero-sum games, especially in competitive environments like trading or gambling, skillful strategy and informed decision-making are crucial for gaining an edge over the competition.

Video – What is a Zero-Sum Game?

This educational video, from our sister channel on YouTube – Marketing Business Network, explains what ‘Zero-Sum Game’ means using simple and easy-to-understand language and examples.